Geometry of Tesseract

Elements of the Tesseract

• Vertices: 16
• Edges: 32
• Faces: 24 squares
• Cells: 8 cubes

Geometric properties of parachoron series

• Parachoron (short for parallel octachoron): Every face is parallelogram, every cell is parallelpiped;
• Testoid (short for tesseractoid): Every face is rectangle, every cell is cuboid;
• Tesseract: Every face is square, every cell is cube.

A unit tesseract in Cartesian coordinate system

Locations of vertices:

• A(0,0,0,0), B(1,0,0,0), C(1,1,0,0), D(0,1,0,0), E(0,0,1,0), F(1,0,1,0), G(1,1,1,0), H(0,1,1,0);
• A'(0,0,0,1), B'(1,0,0,1), C'(1,1,0,1), D'(0,1,0,1), E'(0,0,1,1), F'(1,0,1,1), G'(1,1,1,1), H'(0,1,1,1).

Distances of two vertices:

• There are four distances between two vertices: \(1, \sqrt{2}, \sqrt{3}, 2\);
• Where the pair of vertices with distance 2 is the furthest apart: such as A-G', A'-G, B-H', D-F'.
• Any diagonal line of length 2 crosses the center point, (0.5,0.5,0.5,0.5).

Projection:

Before we explore the tesseract, let's familiarize ourselves further with the orthogonal projection of it, which we'll rely on in the following discussion. This projection is actually pretty easy to draw, start by drawing those four perpendicular lines in the center, then patch them into a square, and then connect the remaining lines.

First, we have to find these eight cube cells. I drew one of them, ABCD-EFGH, with red lines. That cell resides in the realm u=0. There's another cube, A'B'C'D'-E'F'G'H', connected to the red cube at their corresponding vertices. Other 6 cubes are in between corresponding faces of the two cubes, such as ABCD and A'B'C'D'. This projection reflects the fact that all cells of the tesseract are congruent.

Positional relationships with realms

The diagrams below show some lines, planes, and realms in relation to the red cell. In fact, all relationships with cells are simple enough to use analogies.

Line-cell: perpendicular. E.g. line BB' and the red cell. We can prove that BB' is perpendicular to all the lines in the realm u=0 (using the vector method, all the vectors in the realm can be represented as a linear superposition of AB, AD, and AE, and then it's easy). In this case, we say that BB' is a normal of the cell.

Line-cell: parallel. E.g. line B'C' and the red cell. In 3D geometry we know that if a line is parallel to any line in the plane, then it is parallel to that plane. An analogy can be made to 4D space, i.e., B'C' is parallel to the red cell because BC//B'C'.

Line-cell: oblique intersection. E.g. line BA' and the red cell. Since AA' is a normal line of the red cell, the projection of BA' is BA. Thus, the line-cell angle is 45°. Simple, isn't it?

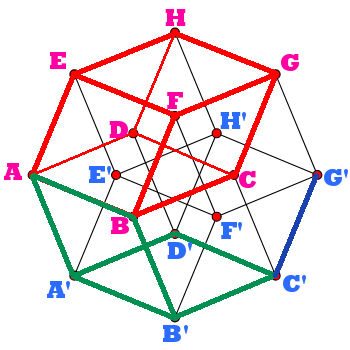
Face-cell: perpendicular. E.g. face ABB'A' and the red cell intersect on the line AB. The face-cell angle is 90 degrees because AA'⊥AE.

Face-cell: parallel. E.g. face A'B'C'D' and the red cell.

For a plane that intersect obliquely, such as BFG'C' (not pictured in the figure), we can also use the definition to calculate its face-cell angle as 45 degrees. Since the cells (realms) have normals, the projective area theorem can be used to calculate the face-cell angle.

Two cells: perpendicular. E.g. cell ABCD-EFGH and cell ABCD-A'B'C'D' (realm u=0 and z=0) intersect on plane ABCD.

Two cells: parallel. E.g. cell ABCD-EFGH and cell A'B'C'D'-E'F'G'H' (realm u=0 and u=1).

Line-face: disjoint. E.g. face ABCD and line C'G'. These are not parallel or intersecting. We can translate the line C'G' to CG, making it share the realm with face ABCD.

Various positional relationships

Points:

Two points determine a straight line. Three non-linear points determine a plane. Four non-planar points determine a realm.

Two lines:

Two straight non-planar lines determine a realm. (Think about why.) So there are 3 cases: parallel, intersecting, and disjoint. The two-line-angle has been defined long ago, and we can do the math.

Various theorems:

• For a line L and a point P, there's a line parallel to L and crosses P.
• If L1//L2 and L1//L3, then L2//L3.
• In 4D, there exists a sphere that has no common point with a straight line, and the center of the sphere is on that line. e.g., the line \(x=y=z=w\) and a sphere \(w=0，x^{2}+y^{2}+z^{2}=1.\)

A line and a plane:

There are three cases:

• Disjoint: 1) No common points. 2) Not parallel. 3) Non-realmic. 4) May be perpendicular.
• Parallel: 1) No common points. 2) Every point on the line is in the same distance from the plane.
• Intersect: 1) Has one common point. 2) May be perpendicular.

If a line and a plane are disjoint, we can translate the line to the realm where the plane is. It gives the line-plane angle. cf. two disjoint lines in 3D.

Various theorems:

(P is a point, L is a line, S is a plane.)

• For P not on S, there are infinitely many lines over P and perpendicular to S. Only one of them and S share a realm.
• For P not on L, there are infinitely many planes over P and perpendicular to L. Only one of them and L share a realm.
• For P on S, there are infinitely many lines over P and perpendicular to S. Any of them and S share a realm.
• For P on L, there are infinitely many planes over P and perpendicular to L. Any of them and L share a realm.

Realm theorem:

• Four non-planar points form a tetrahedron; they determine a realm.
• Corollary 1: A plane and a point outside the plane determine a realm.
• Corollary 2: Two parallel planes determine a realm.
• Corollary 3: Two intersecting planes determine a realm.
• Corollary 4: Two disjoint lines determine a realm.

A line and a realm:

• Parallel: 1) No common point. 2) Every point in the line is in the same distance from the realm.
• Intersect: 1) Has one common point. 2) May be perpendicular.

By projecting the line on the realm, we can do the math to get the line-realm angle. cf. line-plane angle in 3D.

A plane and a realm:

• Parallel: 1) No common point. 2) Every point in the plane is in the same distance from the realm.
• Intersect: 1) Share a line. 2) May be perpendicular.

Define the plane-realm angle as the angle between two lines perpendicular to the line of intersection in the plane and in the realm.

Two realms:

• Parallel: 1) No common point. 2) Every point in the realm is in the same distance from another realm.
• Intersect: 1) Share a plane. 2) May be perpendicular.

Two realms intersect on a plane, so the two-realm angle, usually called the dichoral angle, can be defined as the angle between two straight lines perpendicular to the intersecting plane in each realm.

Two planes

This is the most complicated one in 4D. We already know two cases where the planes are corealmic:

• Parallel: 1) No common point. 2) Every point on a plane is in the same distance from another plane.
• Intersect: 1) Share a line. 2) May be perpendicular.

In 4D, two new cases appear:

• Disjoint: 1) No common point. 2) Not parallel. 3) May be half perpendicular. 4) Non-realmic.
• Contact: 1) Have only one common point. 2) May be half perpendicular or absolutely perpendicular. 3) Non-realmic.

Theorems of parallel planes:

• For P and S, there exists one plane which passes over P and is parallel to S;
• If S1//S3 and S2//S3, then S1//S2.
• If two planes are disjoint, we can translate one of them so that they have an intersection line.
• If two planes intersect in a point, no matter how we translate one of them, they intersect in a point.

Absolutely perpendicular (or completely orthogonal) planes:

• Two planes have only one common point;
• E.g., xy-plane: \(z=0, w=0\) and zw-plane: \(x=0, y=0\) intersect at the origin;
• If we choose a line in each of the planes, the two lines are always perpendicular;
• For a point and a plane, there exists one plane which is over the point and is absolutely perpendicular to the first plane;
• If S1 is absolutely perpendicular to S2, we say S1 is the normal plane of S2;
• If two vectors intersect and both are perp to S1, then the plane made by the two vectors is the normal plane of S1.

Various theorems:

• In 4D space, there exists a circle that has no common point with a plane, and the center of the circle is in that plane. e.g., plane: \(x=y=z\); circle: \(w=0，z=0，x^{2}+y^{2}=1\).

Two-plane angle:

The angle between two planes is a bit tricky.

• One value is not enough to describe the angle between two planes in 4D space. Two values are necessary;
• Take a line on a plane S1. The line-plane angle between the line and S2 take in a range of \(\theta_{1}\) and \(\theta_{2}\);
• Take a unit circle on S1, then project it on S2. The circle turns into an ellipse. The short radius and long radius of that ellipse represent \(\cos\theta_{1}\) and \(\cos\theta_{2}\), respectively;
• This is the idea of a method called the "unit circle method" for finding the angle. It deals with ellipses using cumbersome methods such as quadratic linear algebra, though.

Examples of two-plane angles:

• If S1//S2, any line on S1 form the line-plane angle 0° with S2. Thus, \(\theta_{1}=\theta_{2}=0°.\)
• If S1 and S2 intersect in a line and form a dihedral angle, \(0<\theta_{1}≤90°,\theta_{2}=0°.\)
• If the two angles are non-zero, the planes intersect in a point.
• Particularly, if \(\theta_{1}=\theta_{2}\), we call it isoclinic.
• If S1 and S2 are absolutely perpendicular, since any two lines on each plane are perpendicular, the projection on S2 of any point on S1 falls at the point where their feet are located. Thus, \(\theta_{1}=\theta_{2}=90°\).
• If two planes are disjoint (skew), \(\theta_{2}=0°\).
• If \(\theta_{2}=0°\), two planes share a realm, or they are disjoint.
• If \(\theta_{1}=90°\), we call it half-perpendicular.

Situations of two perpendicular planes:

• Half-perpendicular and intersect in a line;
• Half-perpendicular and intersect in a point;
• Absolutely perpendicular;
• Half-perpendicular and disjoint;

Normals:

• 1+1=2; thus, in 2D, a line has a normal line;
• 1+2=3; thus, in 3D, a plane has a normal line;
• 1+3=4; thus, in 4D, a realm has a normal line;
• 2+2=4; thus, in 4D, a plane has a normal plane.

Thinking questions:

Starting with this series of articles, I will end each article with a simple question, so you can try to see how well you understand the contents. The answer will be published in the following article.

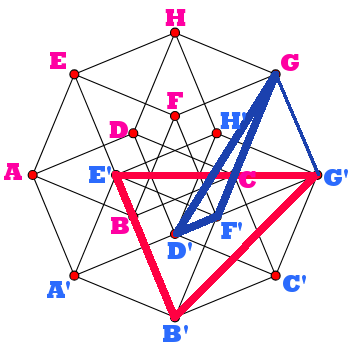
1) Draw the normal plane (absolutely perpendicular plane) of the red plane.

2) Draw the normal plane of the blue plane.

Other stuff

Okay, now let's explore some interesting facts of the tesseract.

Cross sections of the tesseract

Verify that any four points define a cell: any four non-coplanar vertices in a hypercube define a cell. Just like in three-dimensional geometry, sometimes the tetrahedral cell made of these four points is not a complete cross-section.

Under construction

Go back