We are familiar with three directions, which are front-back, left-right, and up-down. Adding another independent axis to them gives the four-dimensional space. In this laboratory, we will explore various figures in 4D space and their geometric properties, some of which are natural extensions of 3D figures, and some of which are unique to 4D.
Let us begin with prisms. For any 2D shape, we can build a prism in 3D by moving the shape along the third direction. This operation is called extrusion. We can build a prism in 4D by taking a 3D object and translating it in a different direction from the realm (3D space; usually called hyperplane) in which the object resides.
Just like the cube is a prism based on a square, a 4D hypercube, also called a tesseract, is a prism based on a cube. It has following properties:
A 3D prism has rectangles as side faces, which are formed by translating edges of the base 2D shape. A 4D prism's "side cells" are prisms based on faces of the base 3D shape. For example, the tetrahedral prism consists of two tetrahedra and four triangular prisms. In the diagram below, brown lines represent lines that extend in the fourth direction:
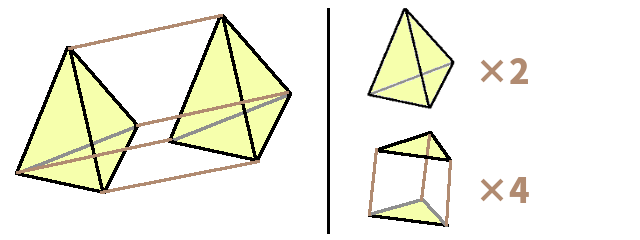
This is another example: the prism based on the truncated tetrahedron, one of semiregular polyhedra. This time, one of truncated tetrahedra is drawn inside the other. Its side cells are 4 triangular prisms and 4 hexagonal prisms.
Just like the volumes and surface areas of 3D prisms, we can determine the bulks and surcell volumes of 4D prisms. Base volume \(V\), base surface area \(S\), height \(h\), bulk \(T\) and surcell volume \(C\) fit the following formulas:
・\(T=Vh\)The cylinder consists of two circles as bases, and one curved surface which connect the circles. A rectangle is formed by cutting and flattening the curved surface along its base line. What is the structure of a prism whose base is a cylinder, i.e., a cylindrical prism? Which cells are in between two cylinders? Another two cylinders, and one "curved cell." When we cut open the curved cell of a cylindrical prism, we get a cuboid!
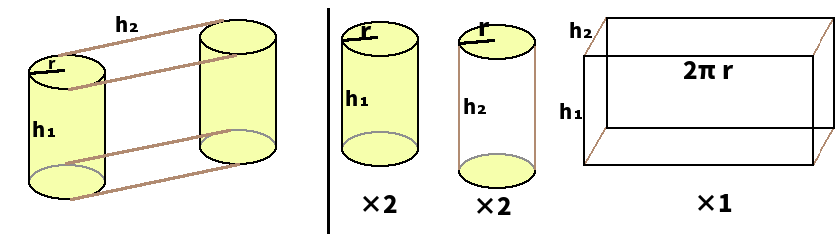
The bulk of the cylindrical prism is given by \(\pi r^{2}h_{1}h_{2}\), and the surcell volume \(2\pi r^{2}(h_{1}+h_{2})+2\pi rh_{1}h_{2}\), where \(h_{1}\) is the height of the base cylinder, \(r\) is the base radius, and \(h_{2}\) is the height along the fourth direction.
When you look closely at the diagram or formulas above, you'll notice that \(h_{1}\)& \(h_{2}\) are in the same positions. Therefore, it's fine to consider any of the four cylinders as the base of a cylindrical prism.
We can think of a cylinder as the limit of an n-gonal prism as n approaches infinity. N-gonal prismatic prism consists of 4 n-gonal prisms and n cuboids. For example, if n = 4, we have a tesseract or a testoid. The following figure shows the projection of a decagonal prismatic prism:
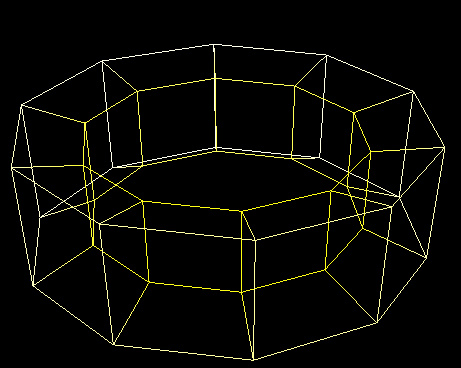
Looking at the image, it seems that 4 decagons connect each other to form 10 squares. Let's try something new: create 10 triangles by muscling 3 decagons together.
Is this a 4-dimensional figure? The answer is "yes," but of course, it is no longer a prism. In fact, it can be interpreted from the viewpoint of a direct product. I will tell you more about it later.
Some 4D shapes don't have a "net." The spherinder, a prism based on a sphere, is one of them. Two spheres connect by one curved cell. What are the bulk and surcell volume? Here a problem arises: since a sphere surface cannot be flattened into a plane, the side cell of a spherinder cannot be "flattened" into a 3D shape. Nevertheless, we can calculate its surcell volume by the integral method, just like the surface area of a sphere, \(4\pi r^{2}\). The bulk and surcell volume are given by \(\frac{4}{3}\pi r^{3}h\) and \(\frac{4}{3}\pi r^{3}\times2+4\pi r^{2}h\) respectively, where \(r\) is the radius and \(h\) is the height.
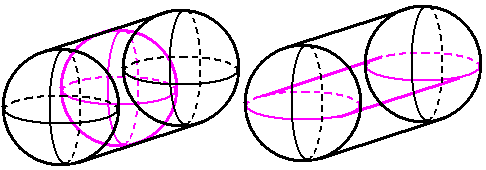
In the future, we will analyze how the spherinder and the cylindrical prism roll on a tabletop in the 4D world and experience the wonder of the 4D world.
A 4D pyramid is a figure formed by connecting each vertex of any 3D figure to a point not in the same realm. Its side cells are pyramids based on faces of the base cell.
Example: The cubic pyramid has side cells of 6 square pyramids and side faces of 12 triangles.
What are the bulks of 4D pyramids? In 3D, we learned a pyramid's volume is a third of a prism's by dividing a cube into 6 identical pyramids. By analogy, we can guess that a tesseract can be divided into 8 cubic pyramids. Therefore, the bulk of a 4D pyramid is a fourth of the corresponding 4D prism. In n-dimension, it's \(\frac{1}{n}\). These are not sufficient as proofs, and an accurate proof requires integration. I omit them here.
Cylindrical prism, cylindrical pyramid, conical prism, conical pyramid:
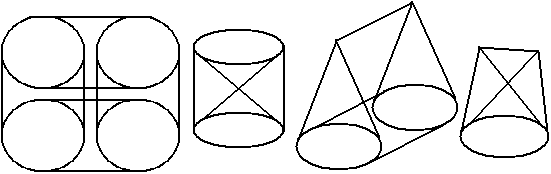
Can you tell which cells they are surrounded by? How do the cells connect to each other? Their bulks are given by:
\(V_{1}=\pi r^{2}h_{1}h_{2},V_{2}=\frac{1}{4} \pi r^{2}h_{1}h_{2},V_{3}=\frac{1}{3} \pi r^{2}h_{1}h_{2},V_{4}=\frac{1}{12} \pi r^{2}h_{1}h_{2}\)What about the surcell areas?
For any n-dimensional shape, we can think of a prism or pyramid which has it as the base. It would be an (n+1)-D shape. We can imagine that there must be the cylindrical prism prism pyramid pyramid, the conical prismatic pyramidic prismatic pyramidic prism, and so on, in high-dimensional spaces. Fortunately, we are not in those crazy dimensions!
Pyramid pyramid prism prism, prism prism pyramid pyramid... Do you understand?
Congrats! You already have a 4D civilized elementary school student's understanding of geometric figures! The next time, we will learn geometry in junior high, let's read works written by Euclid in their civilization!
Note: Some of the names may cause confusion, i.e., the "truncated tetrahedral prism" is ambiguous between "(truncated tetrahedral) prism" and "truncated (tetrahedral prism)." We need to come up with a solution.