Dihedral angle

In 3D and above, a dihedral angle is the angle between two planes. For instance, any 2 faces of the cube form the dihedral angle of 90°.

The dihedral angle is defined as the angle between two normal vectors.

In this article, we'll discuss how we can find the dihedral angles of the regulars in 3D.

There's a powerful property of regulars: the normal vector of a face is the vector from the center of the polyhedron to the center of that face.

In the following diagram, the red arrows are normal vectors of faces ACD & BCD of a Tet. They start at the center of the Tet, crossing the centers of the faces.

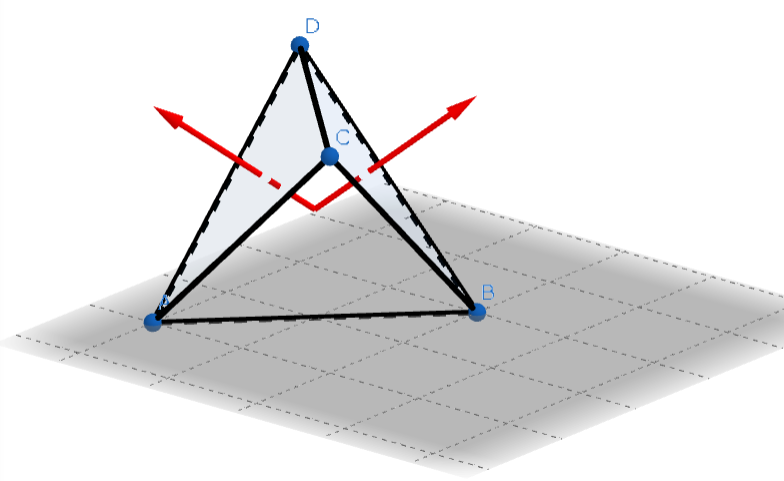
The angle between the two vectors - about 109.47° - is the supplementary angle of the angle between the two faces. Thus, the dihedral angle of the Tet is about 70.53°.

How to find the angle

A clever way to find the dihedral angle of a regular is to utilize two things:

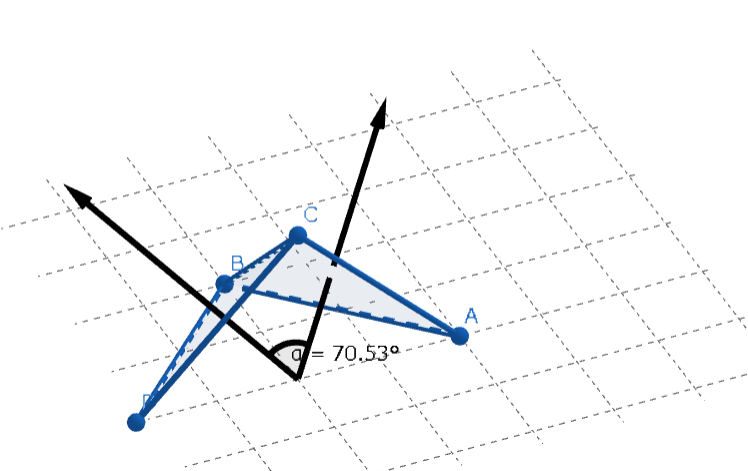
The inner product method of vectors. A benefit of the inner product is that we can easily find the cosine value of the angle between two vectors.
The dual relationships. For regular and semiregular polyhedra, the center of a face corresponds to a vertex of the dual polyhedron. This means a normal vector of a face is a vector to a vertex of the dual.

Let's think about a Tet which has 4 vertices at \(A(1,1,1), B(-1,-1,1), C(-1,1,-1), D(1,-1,-1)\). The center is \(O(0, 0, 0)\). Since the Tet is self-dual, we don't have to take its dual. Just choose two adjacent vertices, such as \(A\) and \(B\). Let \(\theta\) be the angle between \(OA = [1, 1, 1]\) and \(OB = [-1, -1, 1]\). Find \(\theta\) using the inner product:

\(\cos \theta = \frac{OA \cdot OB}{|OA||OB|} = - \frac{1}{3}\)

\(\Rightarrow \theta = \arccos (-\frac{1}{3})\)

Thus, the dihedral angle of the Tet is its supplementary angle, \(\arccos\frac{1}{3}\).

Alternative method

Another way to find the center of a face is adding all vertices. It works as long as the face is regular. In the above example, the normal vector of face \(ABC\) is \(OA[1,1,1]+OB[-1,-1,1]+OC[-1,1,-1] = [-1,1,1].\)

Cube, Oct

The cube and Oct are duals.

The 8 vertices of a cube is represented below:

\((\pm1, \pm1, \pm1)\)

The 6 vertices of an Oct is represented below:

\((\pm1, 0, 0)\) and its permutations

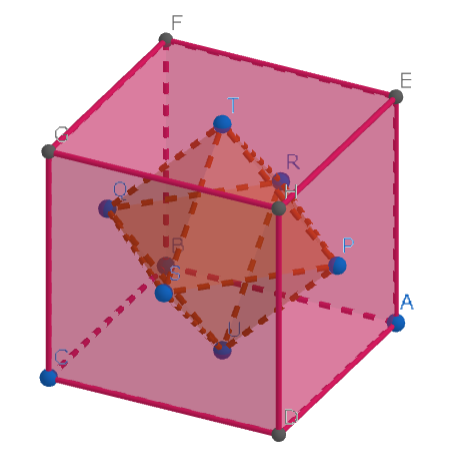
We can verify that the dihedral angle of the cube is 90° by taking its dual, the Oct. Any two adjacent vertices of the Oct forms the angle of 90°.

Similarly, we can find the dihedral angle of the Oct by thinking about its dual, the cube. It's the angle between two vectors, \([1, 1, 1]\) and \([1, 1, -1]\) for example. The answer is \(\arccos (-\frac{1}{3})\) - the supplementary angle of the Tet's dihedral angle.

The following diagram shows only two faces of an Oct.

Doe, Ike

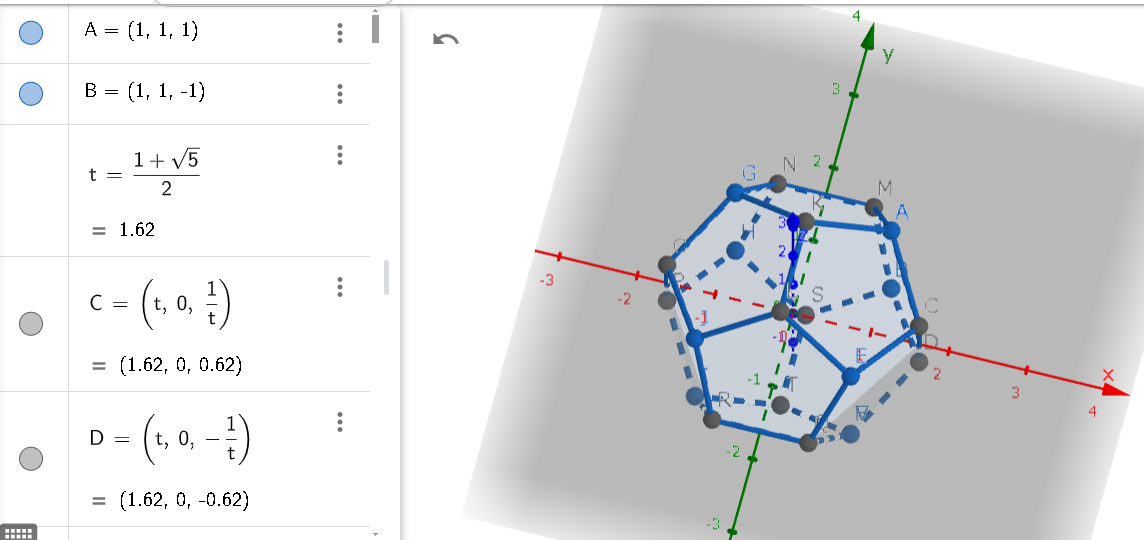
The Doe and Ike are duals.

The 20 vertices of a Doe is represented below:

\((\pm1, \pm1, \pm1)\) (8 points)
\((\pm\tau, 0, \pm\frac{1}{\tau})\) and its even permutations (12 points)

Here, \(\tau\) is the golden ratio, \(\frac{1+\sqrt{5}}{2}.\)

In this case, the edge length is \(\frac{2}{\tau}.\)

The 12 vertices of an Ike is represented below:

\((\pm\tau, \pm1, 0)\) and its even permutations (12 points)

In this case, the edge length is 2.

Dihedral angle of Doe

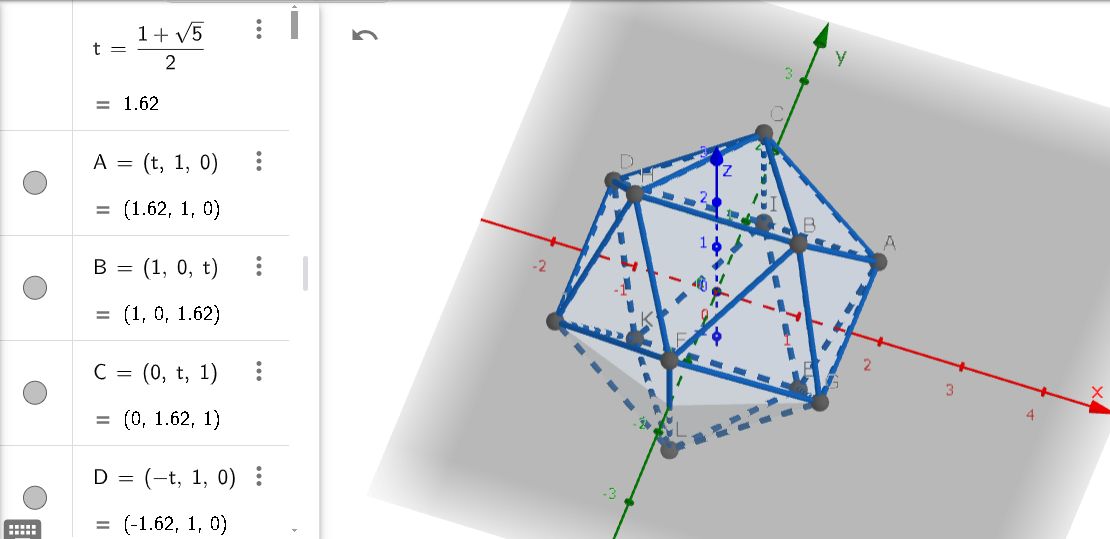
\(A(\tau,1,0)\) and \(B(\tau, -1, 0)\) are adjacent vertices of an Ike.

Let \(\theta\) be the angle between \(OA\) and \(OB.\)

\(\cos\theta = \frac{\tau^{2}-1}{\tau^{2}+1}=\frac{\tau}{\tau+2}=\frac{\sqrt{5}}{5}\)

Thus, the dihedral angle of a Doe is \(\arccos (-\frac{\sqrt{5}}{5}).\)

Dihedral angle of Ike

\(A(1,1,1)\) and \(B(\tau, 0, \tau^{-1})\) are adjacent vertices of a Doe.

Let \(\theta\) be the angle between \(OA\) and \(OB\).

\(\cos\theta = \frac{2\tau-1}{3}=\frac{\sqrt{5}}{3}\)

Thus, the dihedral angle of an Ike is \(\arccos (-\frac{\sqrt{5}}{3}).\)